
Indhold
- Zipf's lov forklaret
- Grundlæggende eksperiment
- Zipfs lov på dampmarkederne
- Hvad kan vi lære om Steam?
- konklusioner
For en kort tid siden foreslog en ven af mig, at jeg kigger på Vsauces-video om Zipfs lov, Paretos princip og deres mystiske fremtoninger rundt om os. Her er en lille teaser for at få din opmærksomhed - 80% af alle mennesker bor i 20% af de mest populære byer; 80% af alle arealer tilhører 20% af de rigeste udlejere 80% af alt affald er på de øverste 20% sårbare gader - som forudsagt af Zipfs lov og Paretos-princippet.
Ikke nok? Nå, da jeg opdagede i går, stopper kaninhullet ikke der ... Fuld skepticisme, jeg besluttede at se på hvor meget tid folk bruger til at spille dampspil ... Nå. 80% af folks tid bruges til at spille 20% af de mest populære spil ... Interessant? Nå, læs videre, der er mere til denne historie.
Indsøgning på over 20 minutter, Vsauces bestræbelser er fantastisk og forklarer mange af de store billedspørgsmål om Zipf, men han er meget genert for at vise os kernemekanismen, der bredt antages at bidrage til, hvorfor Zipf arbejder, hvordan det gør. Så inden vi går videre, vil jeg gerne kortfattet forklare det.
Zipf's lov forklaret
Der er flere konceptuelle måder at forklare intuitionen bag 20/80 princippet. Det bedste eksempel er efter min mening den ene om månekratere.
Grundlæggende eksperiment
Så forestill dig, om du vil, at der er en uberørt Månen - en perfekt glat overflade. Nu skal du sige, at der er nogle tilfældigt mellemstore asteroider, der ramte Månen. Når den første asteroide lander, forlader den et krater. Nu rammer en anden en krater andetsteds. Hvert krater er en del af det samlede overfladeareal, derfor er der en chance for, at den næste tilfældige asteroide vil ramme tæt på et eksisterende krater og slutte sig til det, og danne en gruppe. Chancen for en ny asteroide, der rammer et givet krater, er så proportional med kraters og asteroidernes eksisterende størrelse. Det betyder, at den næste tilfældige asteroide er mere tilbøjelig til at blive med i den største eksisterende gruppe, hvilket gør den endnu større. En slags kumulativ proces, der så skaber en rig-get-rigere dårlig-få-ensom mekanisme.
Husk på det, fordi det antages at være den generelle forklaring på "hvorfor" Zipfs lov arbejder med sådan mystisk universalitet. Asteroideeksemplet er ret simpelt, men spørgsmålet er, hvad der vil ske over mange gentagelser
Lidt forvirrende?
Nå, jeg lavede et gif til at køre dette indledende punkt hjem. NB! grafen vil blive diskuteret senere, prøv bare og billedet eksperimentet.

Hvis vi observerer den faktiske Månen, viser det sig, at da mængden af asteroider stiger til store mængder, bliver de observerede kraterdiametre vokset således, at de øverste 20% af de største kratere nærmer sig 80% af hele overfladearealet.
Så når vi går til flere asteroider nærmer fordelingen af de mest populære til mindst populære grupper en form for "ideel distribution" med denne 20/80 ejendom - en Pareto-distribution. Hvis du laver matematikken, viser det sig, at (generelt), hvis den største gruppe har størrelse N, er den næststørste gruppe omkring størrelse N / 2, den tredje N / 3 og så videre og så videre. Dette kaldes Zipfs lov. Den underlige ting er Zipfs lov og Pareto-distribution virker for en forvirrende mængde elementer (asteroider) og grupper (kraterklynger). Selvfølgelig er der skævheder og tilfældige forstyrrelser, men den generelle tendens er ubestridelig.
Jeg håber du kan se, hvordan asteroider er mere tilbøjelige til at ramme store kratere på månen, forbinder at byer bliver mere attraktive, hvis der allerede er flere mennesker der bor i dem. Men man må indse, at byer er langt fra de eneste "grupper", der opfører sig i henhold til Zipf.
Her er nogle eksempler fra Mark Newmans forskning om Pareto distributioner. NB! Graferne er i log-log-skala, som udjævner kurvens hyperboliske form og viser en næsten lineær relation.
Indledende y = aX ^ (- b)
Log af begge sider => log y = log a - b log X
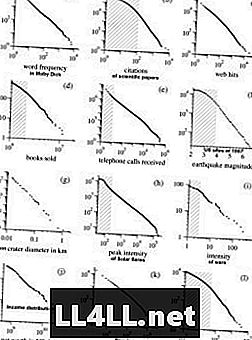
Interessant nok vises den samme tendens også af religiøse kulturer. Den fælles ejendom i de fleste af disse fænomener er simpelthen denne "store grupper-større" tendens. Så Zipfs lov er vedholdende i mekanismer, hvor elementernes præferencer er positivt forbundet med gruppens størrelse (dvs. jo større gruppen jo mere sandsynlig vil den vokse). Derfor tænker jeg på grupper som klynger og elementer som klynger.
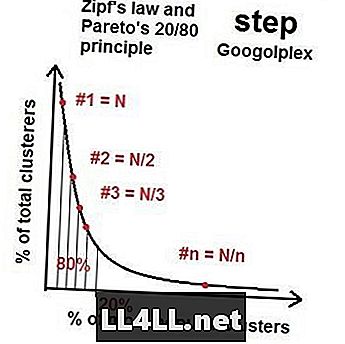
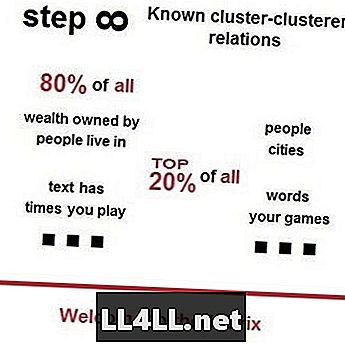
Zipfs lov på dampmarkederne
Mistænkelig for den sidste? Her er den tid, folk bruger på de mest populære spil på Steam. Data fra SteamSpy.
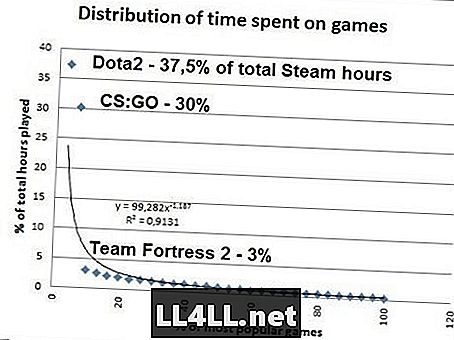
Hvis du gør matematikken, viser det sig, at 20% af de mest populære Steam-spil tegner sig for 80% af det samlede antal spil, så Pareto 20/80 mysteriet virker som en charme her ... Man skal dog bemærke, at Zipf at være sandt, CS: GO skal tegne sig for 37,5% / 2 = 18,8% af den samlede tid i stedet for en kæmpe 30%. Men bortset fra denne outlier (STOP PLAYING CS: GO) er den Zipf-lignende distribution helt klart der.
Her er mængden af kopier solgt til de mest populære spil.
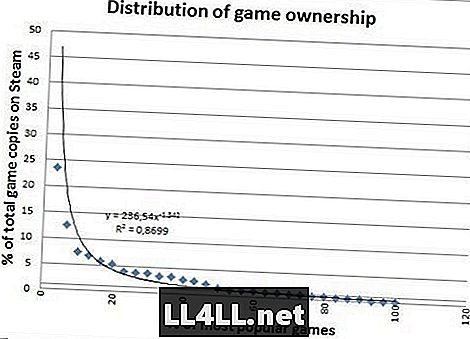
Ser meget pænere eh? Eksemplarer, der sælges, har ikke store outliers, så det passer meget godt, hvilket er en bemærkelsesværdig forskel. Der er dog noget mere interessant at konkludere med forskellene i de sidste to grafer.
Kan du bemærke, hvordan "halen" til højre er lidt fed i anden graf? Tja, med enkle ord betyder det, at de "relativt upopulære" spil faktisk er meget mere populære end i det forrige plot.
Faktisk viser det sig, at 20% af de mest populære spil tegner sig for kun 60% af salget, mod 80% af spillet. Interessant? Du spytter din røv, det er.
Hvad kan vi lære om Steam?
Vel, at spillet popularitet følger Pareto distribution fortæller os, at der faktisk er en slags positiv netværkseffekt, hvilket gør spillerne vælge spil, der allerede bliver spillet af flere mennesker. Hvad forskellen i fedthed af haler fortæller os er, at Steam-brugere er meget mere "gruppe-size-blind", når de køber spil, end de er, når de spiller dem.
Tænk på det - jo flere mennesker køber spil uanset "nuværende populære mening", jo mere udfladte Pareto-distributionen kommer, da det er mindre sandsynligt for store spil at vokse yderligere. Hvis ingen gav en rotter røv om hvor mange mennesker der allerede spiller et spil, og tilgængeligheden af alle spil var den samme, så ville vi forvente, at 20% af de mest populære spil skulle tegne sig for omkring 50% af salget og spilletiden (fx hvis man antager individuelle præferencer er normalt fordelt).
konklusioner
Så der er to faktorer, der bidrager til Pareto-distributionen på Steam-markederne - hvor innovativt udviklerne er (hvor mange nye månekratere bliver dannet) og hvor meget spillere (asteroider) værdiansætter den nuværende gruppestørrelse, når de vælger hvilken gruppe der skal deltage . Som det viser sig, er spillere meget gruppe-size-blind, når de køber spil, men bare det modsatte, når de spiller dem. Cool huh?
Hvis du vil lære mere om Zipfs lov- og magtlovsfordelinger, er her et godt foredrag. Desuden skal du kigge på Newman's papir!
Hvis du vil læse mere af denne slags ting, vil jeg snart nok forsøge at deltage i denne observation til en model, hvilket viser, at mere populære multiplayer-spil har højere priser (som linker til spillerens præference for at blive med i større grupper). Se artiklen her. Piece De Resistance-artiklen vil forsøge at slutte sig til disse teorier sammen og forklare, hvordan multiplayer-spil, sociale netværk og byer faktisk er alle anti-rivaliserende varer med netværkseffekter (jo flere mennesker bruger et godt, jo mere er hver enkelt forbrugerfordel), som har berettiget dem med denne Zipfian tåge af mysterium ...
Indtil da - nyd jer!
P. S. Pop i en kommentar med en sjov idé for en 20/80 relation, du tror måske være sandt.
Mine er:
80% af befolkningenes nostalgi skyldes 20% af deres lykkeligste minder (faktisk bevist for den rate folk glemmer oplysninger på)
80% af massen er koncentreret i 20% af de største rumgenstande (faktisk bevist for distribution af tyngdekraften)
Og selvfølgelig
80% af rodet på dit toilet kommer fra 20% af hvad du spiser (ingen akademisk forskning til at tale om)